A simple pendulum with a bob of mass $m$ is suspended from the roof of a car moving with a horizontal acceleration $a.$ Then

A simple pendulum with a bob of mass $m$ is suspended from the roof of a car moving with a horizontal acceleration $a.$ Then 
A. The string makes an angle of ${\tan ^ – }\left( {\frac{a}{g}} \right)$ with the vertical.
B. The string makes an angle of ${\tan ^ – }\left( {1 – \frac{a}{g}} \right)$ with the vertical.
C. The tension is the string is $m\sqrt {{a^2} + {g^2}} $
D. The tension in the string is $m\sqrt {{g^2} – {a^2}} $
Solution

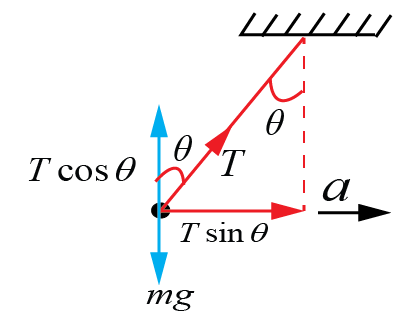
$$T\cos \theta  = mg$$ $$T\sin \theta  = ma$$ $$\therefore \quad \tan \theta  = \frac{a}{g}$$ $$\quad \quad \theta  = {\tan ^ – }\left( {\frac{a}{g}} \right)$$ Tension in the string, $$T = m\sqrt {{g^2} + {a^2}} $$  

Hence options (A) and (C) are the correct answers.