The force of buoyancy exerted by the atmosphere on a balloon is $B$ in the upward direction and remains constant. The force of air resistance on the balloon acts opposite to the direction of velocity and is proportional to it. The balloon carries a mass $M$ and is found to fall down near the earth’s surface with a constant velocity $v .$ How much mass should be removed from the balloon so that it may rise with a constant velocity $v$?
(A) $2\left\{ {M + \frac{B}{g}} \right\}$
(B) $2\left\{ {M – \frac{B}{g}} \right\}$
(C) $\left\{ {M + \frac{B}{g}} \right\}$
(D) $\left\{ {M – \frac{B}{g}} \right\}$
The correct answer is B. $2\left\{ {M – \frac{B}{g}} \right\}$
Solution:
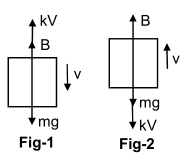
Let, the air resistance force is $F$ and Buoyant force is $B$. Given that
$${F}_{a} \propto {v},$$ where ${v} \rightarrow$ velocity
$$\Rightarrow F_{a}=k v,$$ where $k \rightarrow$ proportionality constant When the balloon is moving downward,
$${B}+{kv}={Mg} \quad …(i)$$
$$\Rightarrow M=\frac{B+k v}{g}$$
For the balloon to rise with a constant velocity ${v}$, (upward) let the mass be $m$
Here,
$${B}-({mg}+{kv})=0$$
$$\Rightarrow {B}={mg}+{kv}$$
$$\Rightarrow {m}=\frac{{B}-{kv}}{{g}}$$
So, amount of mass that should be removed,
$$M-m=\frac{B+k v}{g}-\frac{B-k v}{g}$$$$M-m=\frac{B+k v-B+k v}{g}$$$$M-m=\frac{2 k v}{g}$$From equation $(i)$ we get, $$M-m=\frac{2(M g-B)}{g}$$$$M – m = 2\left\{ {M – \frac{B}{g}} \right\}$$
JEE Question Bank
For best collection of JEE Main, JEE Advanced, Class 11 – 12 boards question visit ThinkMerit question bank.

JEE Mock Test
JEE Main, JEE Advanced unlimited mock test. Guaranteed help. Try yourself and witness the difference.

0 Comments